剑指offer专项突击

Posted on Edited on In Word count in article: 10k Reading time ≈ 9 mins.

剑指 Offer 09. 用两个栈实现队列

用两个栈实现一个队列。队列的声明如下，请实现它的两个函数 appendTail 和 deleteHead ，分别完成在队列尾部插入整数和在队列头部删除整数的功能。(若队列中没有元素，deleteHead 操作返回 -1 )

思路：两个栈

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
class CQueue {
    LinkedList<Integer> A,B;
    public CQueue() {
        A = new LinkedList<Integer>();
        B = new LinkedList<Integer>();
    }
    
    public void appendTail(int value) {
        A.addLast(value);
    }
    
    public int deleteHead() {
        if(!B.isEmpty()){
            return B.removeLast();
        }else if(A.isEmpty()){
            return -1;
        }
        while(!A.isEmpty()){
            B.addLast(A.removeLast());
        }
        return B.removeLast();
    }
}

/**
 * Your CQueue object will be instantiated and called as such:
 * CQueue obj = new CQueue();
 * obj.appendTail(value);
 * int param_2 = obj.deleteHead();
 */

剑指 Offer 10- I. 斐波那契数列

写一个函数，输入 n ，求斐波那契（Fibonacci）数列的第 n 项（即 F(N)）。斐波那契数列的定义如下：

F(0) = 0, F(1) = 1
F(N) = F(N - 1) + F(N - 2), 其中 N > 1.
斐波那契数列由 0 和 1 开始，之后的斐波那契数就是由之前的两数相加而得出。

答案需要取模 1e9+7（1000000007），如计算初始结果为：1000000008，请返回 1。

思路：动态规划

1
2
3
4
5
6
7
8
9
10
11
class Solution {
    public int fib(int n) {
        int a = 0 , b = 1 , sum;
        for(int i = 2 ; i <= n+1 ; i++){
            sum = (a + b) %1000000007;
            a = b ;
            b = sum;
        }
        return a;
    }
}
  • 时间复杂度：O（N）
  • 空间复杂度：O（1）

注意：听说字节面试要求时间复杂度：logn

剑指 Offer 10- II. 青蛙跳台阶问题

一只青蛙一次可以跳上1级台阶，也可以跳上2级台阶。求该青蛙跳上一个 n 级的台阶总共有多少种跳法。

答案需要取模 1e9+7（1000000007），如计算初始结果为：1000000008，请返回 1。

思路：动态规划（斐波那契数列）

还是和上一题一样：

此类求多少可能性的题目一般都具有递推性质：即f（n）和f（n-1）…f（1）之间是有联系的。设跳上 n 级台阶有
f(n) 种跳法。在所有跳法中，青蛙的最后一步只有两种情况：

  • 跳上 1 级或 2 级台阶。当为 1 级台阶： 剩 n−1 个台阶，此情况共有 f(n−1) 种跳法；
  • 当为 2 级台阶： 剩 n−2 个台阶，此情况共有 f(n−2) 种跳法。

f(n) 为以上两种情况之和，即 f(n)=f(n−1)+f(n−2) ，以上递推性质为斐波那契数列。和上一题唯一的不同在于初始数字的不同。

1
2
3
4
5
6
7
8
9
10
11
class Solution {
    public int numWays(int n) {
        int a = 1 , b = 1 , sum;
        for(int i = 2 ; i <= n+1 ; i++){
            sum = (a + b)%1000000007;
            a = b ;
            b = sum;
        }
        return a;
    }
}

剑指 Offer 11. 旋转数组的最小数字

把一个数组最开始的若干个元素搬到数组的末尾，我们称之为数组的旋转。

给你一个可能存在 重复 元素值的数组 numbers ，它原来是一个升序排列的数组，并按上述情形进行了一次旋转。请返回旋转数组的最小元素。例如，数组 [3,4,5,1,2] 为 [1,2,3,4,5] 的一次旋转，该数组的最小值为 1。

注意，数组 [a[0], a[1], a[2], …, a[n-1]] 旋转一次 的结果为数组 [a[n-1], a[0], a[1], a[2], …, a[n-2]] 。

思路：二分查找

本题使用二分查找，但需要考虑特殊情况：

如下图所示，寻找旋转数组的最小元素即为寻找 右排序数组 的首个元素 nums[x] ，称 x为 旋转点

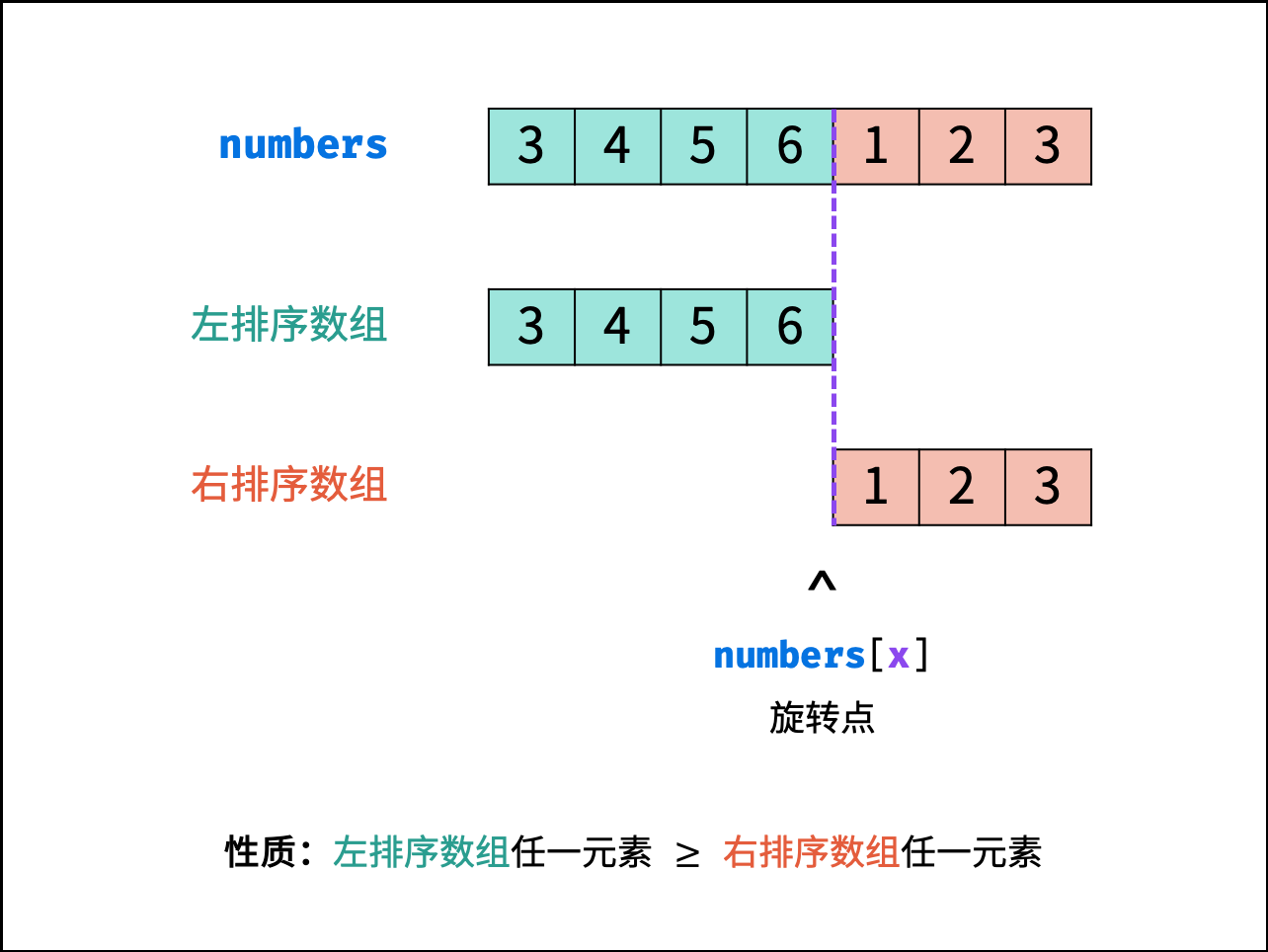
当出现 nums[m]=nums[j] 时，一定有区间 [i,m] 内所有元素相等 或 区间 [m,j] 内所有元素相等（或两者皆满足）。对于寻找此类数组的最小值问题，可直接放弃二分查找，而使用线性查找替代。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution {
    public int minArray(int[] numbers) {
        int i = 0 , j = numbers.length-1;
        while(i < j){
            int m = i+(j-i)/2;//low+high在low和high特别大的时候可能会造成溢出，使用减法避免了溢出发生
            if(numbers[m] > numbers[j]){
                i = m+1;
            }else if(numbers[m] < numbers[j]){
                j = m;
            }
            else{
                int x = i;
                for(int k = i+1 ; k < j ; k++){
                    if(numbers[k] < numbers[x]){
                        x = k;
                    }
                }
                return numbers[x];
            }
        }
        return numbers[i];
    }
}

剑指 Offer 12. 矩阵中的路径

给定一个 m x n 二维字符网格 board 和一个字符串单词 word 。如果 word 存在于网格中，返回 true ；否则，返回 false 。

单词必须按照字母顺序，通过相邻的单元格内的字母构成，其中“相邻”单元格是那些水平相邻或垂直相邻的单元格。同一个单元格内的字母不允许被重复使用。

例如，在下面的 3×4 的矩阵中包含单词 “ABCCED”（单词中的字母已标出）。

思路：深度优先搜索（DFS）+ 剪枝

  • 深度优先搜索： 可以理解为暴力法遍历矩阵中所有字符串可能性。DFS 通过递归，先朝一个方向搜到底，再回溯至上个节点，沿另一个方向搜索，以此类推。
  • 剪枝： 在搜索中，遇到 这条路不可能和目标字符串匹配成功 的情况（例如：此矩阵元素和目标字符不同、此元素已被访问），则应立即返回，称之为 可行性剪枝 。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Solution {
    public boolean exist(char[][] board, String word) {
        char[] words = word.toCharArray();
        for(int i = 0 ; i < board.length ; i++){
            for(int j = 0 ; j < board[0].length;j++){
                if(dfs(board,words,i,j,0)) return true;
            }
        }
        return false;
    }

    public boolean dfs(char[][] board , char[] word , int i , int j , int k){
        if((i < 0 )|| (i >= board.length)||(j < 0 )|| (j >= board[0].length)||(board[i][j]!=word[k])){
            return false;
        }
        if(k == word.length-1){
            return true;//说明都找到了对应的字母
        }
        board[i][j] = '\0';//用来标记已访问的元素，省下了bool[][] visited的空间
        //四个方向都搜索一次
        boolean res = dfs(board,word,i+1,j,k+1)||dfs(board,word,i,j+1,k+1)||dfs(board,word,i-1,j,k+1)||dfs(board,word,i,j-1,k+1);
        board[i][j] = word[k];//还原找过的元素，因为之后可能还会访问到（不同路径）
        return res;
    }
}

剑指 Offer 14- I. 剪绳子

给你一根长度为 n 的绳子，请把绳子剪成整数长度的 m 段（m、n都是整数，n>1并且m>1），每段绳子的长度记为 k[0],k[1]…k[m-1] 。请问 k[0]k[1]…*k[m-1] 可能的最大乘积是多少？例如，当绳子的长度是8时，我们把它剪成长度分别为2、3、3的三段，此时得到的最大乘积是18。

思路：动态规划

令 x 是拆分出的第一个正整数，则剩下的部分是 n−x，n−x 可以不继续拆分，或者继续拆分成至少两个正整数的和。由于每个正整数对应的最大乘积取决于比它小的正整数对应的最大乘积，因此可以使用动态规划求解。

创建数组 dp，其中 dp[i] 表示将正整数 i 拆分成至少两个正整数的和之后，这些正整数的最大乘积。特别地，0 不是正整数，1 是最小的正整数，0 和 1 都不能拆分，因此 dp[0]=dp[1]=0。当 i≥2 时，假设对正整数 i 拆分出的第一个正整数是（1≤j<i），则有以下两种方案：

  • 将i 拆分成 j 和 i−j 的和，且 i−j 不再拆分成多个正整数，此时的乘积是 j×(i−j)；
  • 将 i 拆分成 j 和 i−j 的和，且 i−j 继续拆分成多个正整数，此时的乘积是 j×dp[i−j]。
1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution {
    public int cuttingRope(int n) {
        int[] dp = new int[n+1];
        for(int i = 2 ; i <= n ; i++){
            int curMax = 0;
            for(int j = 1 ; j < i ; j++){
                curMax = Math.max(curMax,Math.max(j*(i-j),j*dp[i-j]));
            }
            dp[i] = curMax;
        }
        return dp[n];
    }
}
  • 时间复杂度：O（n2）
  • 空间复杂度：O（n）

思路2：数学推导

根据数学推导：尽可能将绳子以长度 33 等分为多段时，乘积最大。

  • 最优： 3 。把绳子尽可能切为多个长度为 3 的片段，留下的最后一段绳子的长度可能为 0,1,2 三种情况。

  • 次优： 2 。若最后一段绳子长度为 2 ；则保留，不再拆为 1+1 。

  • 最差： 1 。若最后一段绳子长度为 1 ；则应把一份 3+1 替换为 2+2，因为 2×2>3×1。

1
2
3
4
5
6
7
8
9
class Solution {
    public int cuttingRope(int n) {
        if(n <= 3) return n-1;
        int a = n /3 , b = n %3;
        if(b == 0)  return (int)Math.pow(3,a);
        if(b == 1)  return (int)Math.pow(3,a-1)*4;
        return (int)Math.pow(3,a)*2;
    }
}
  • 时间复杂度：O（1）
  • 空间复杂度：O（1）

剑指 Offer 14- II. 剪绳子 II

给你一根长度为 n 的绳子，请把绳子剪成整数长度的 m 段（m、n都是整数，n>1并且m>1），每段绳子的长度记为 k[0],k[1]…k[m - 1] 。请问 k[0]k[1]…*k[m - 1] 可能的最大乘积是多少？例如，当绳子的长度是8时，我们把它剪成长度分别为2、3、3的三段，此时得到的最大乘积是18。

答案需要取模 1e9+7（1000000007），如计算初始结果为：1000000008，请返回 1。

1
2
3
输入: 2
输出: 1
解释: 2 = 1 + 1, 1 × 1 = 1

思路：数学推导

和前一题一样的思路、理论。

不同之处在于需要在计算过程中取模验算。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
    public int cuttingRope(int n) {
        if(n <= 3) 
            return n - 1;
        int b = n % 3, p = 1000000007;
        long ret = 1;
        int lineNums=n/3;           //线段被我们分成以3为大小的小线段个数
        for(int i=1;i<lineNums;i++) //从第一段线段开始验算，3的ret次方是否越界。注意是验算lineNums-1次。
            ret = 3*ret % p;
        if(b == 0) 
            return (int)(ret * 3 % p);   //刚好被3整数的，要算上前一段
        if(b == 1) 
            return (int)(ret * 4 % p);   //被3整数余1的，要算上前一段

        return (int)(ret * 6 % p);       //被3整数余2的，要算上前一段
    }
}

剑指 Offer 15. 二进制中1的个数

编写一个函数，输入是一个无符号整数（以二进制串的形式），返回其二进制表达式中数字位数为 ‘1’ 的个数（也被称为 汉明重量).）。

思路：巧用n-1

  • (n−1) 解析： 二进制数字 n 最右边的 1 变成 0 ，此 1 右边的 0 都变成
  • n&(n−1) 解析： 二进制数字 n 最右边的 1 变成 0 ，其余不变。

1
2
3
4
5
6
7
8
9
10
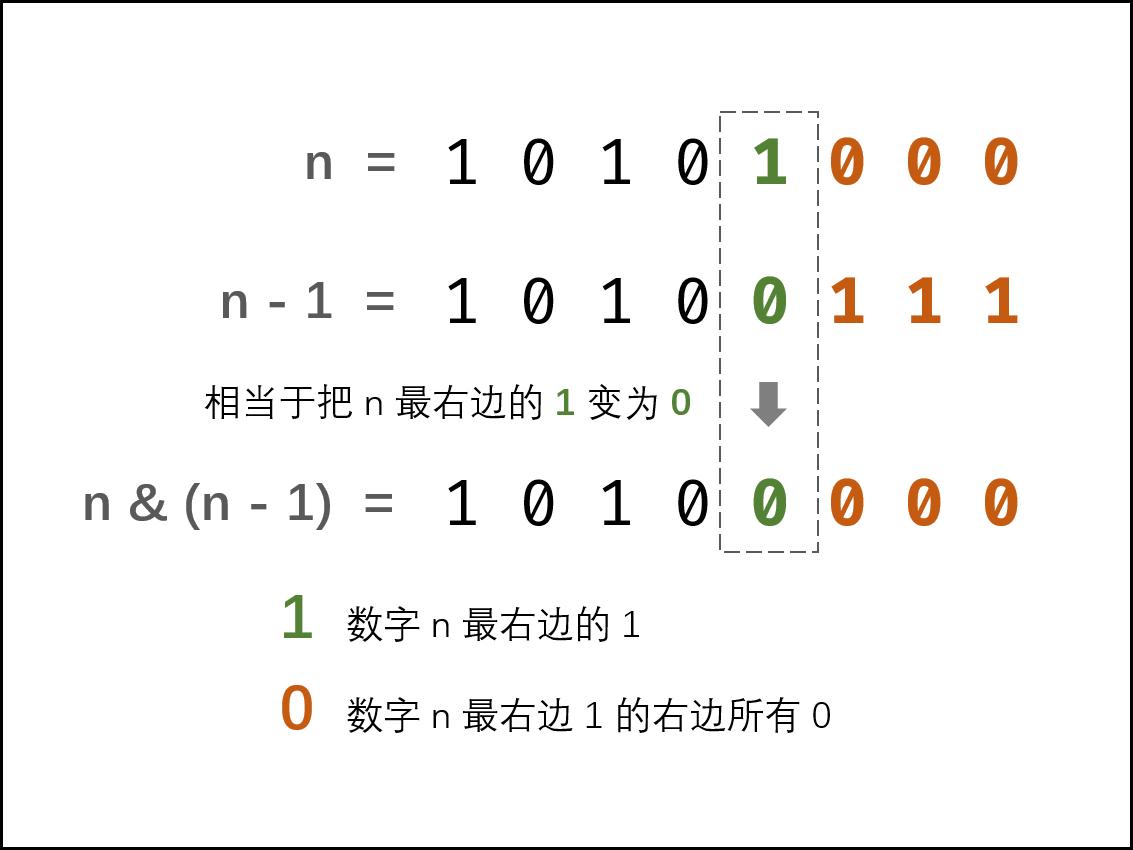
11
public class Solution {
    // you need to treat n as an unsigned value
    public int hammingWeight(int n) {
        int res = 0;
        while(n != 0){
            res++;
            n &= n-1;
        }
        return res;
    }
}

剑指 Offer 16. 数值的整数次方

实现 pow(x, n) ，即计算 x 的 n 次幂函数（即，xn）。不得使用库函数，同时不需要考虑大数问题。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
    public double myPow(double x, int n) {
        if( x == 0 ) return 0;
        long b = n ;
        double res = 1.0;
        if(n < 0){
            x = 1/x;
            b = -b;
        }
        while(b > 0){
            if((b & 1) == 1) res *= x;
            x *= x;
            b >>= 1;
        }
        return res;
    }
}
  • 时间复杂度：O（log2n）：二分的时间复杂度为对数级别
  • 空间复杂度：O（1）

剑指 Offer 17. 打印从1到最大的n位数

输入数字 n，按顺序打印出从 1 到最大的 n 位十进制数。比如输入 3，则打印出 1、2、3 一直到最大的 3 位数 999。

思路：直接模拟

大数越界问题： 当 n 较大时，end 会超出int32 整型的取值范围，超出取值范围的数字无法正常存储。但由于本题要求返回 int 类型数组，相当于默认所有数字都在 int32 整型取值范围内，因此可以不考虑大数越界问题。

1
2
3
4
5
6
7
8
9
class Solution {
    public int[] printNumbers(int n) {
        int end = (int)Math.pow(10, n) - 1;
        int[] res = new int[end];
        for(int i = 0; i < end; i++)
            res[i] = i + 1;
        return res;
    }

思路2：大数打印解法

实际上，本题的主要考点是大数越界情况下的打印。需要解决以下三个问题：

截屏2023-02-21 22.09.29

详解参考

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
class Solution {
    int[] res;
    //start表示该数字当前左边界，这个左边界意思是指当前数字最高位对应的char数组下标。如n=2时，1~9左边界为1，10~99左边界为0
    //nine表示当前数字中出现了多少个9，如果出现1个9，左边界就要向左移1位。例如第1次出现“9”是在9这个数字出现的时候，此时nine++变为1，
    //进入下次递归n为2，nine为1，start为1，此时start就要-1，以便统计二位数字
    int nine = 0, count = 0, start, n;   
    char[] num, loop = {'0', '1', '2', '3', '4', '5', '6', '7', '8', '9'};
    public int[] printNumbers(int n) {
        this.n = n;
        //用来保存最终数字结果的
        res = new int[(int)Math.pow(10, n) - 1];   
        //num数组用来表示字符串，比如n等于2，则num数组为['0''0']、['0''1']、['0''2']...后边是将它转为字符串并按照左边界的位置进行截取的
        num = new char[n];  
        start = n - 1;  //最开始的左边界是从n-1，开始的，因为char数组的下标是从0开始，最末一位为n-1
        dfs(0);   //从char数组的第0位开始
        return res;
    }
    void dfs(int x) {
        //结束条件：当前x的下标越过char数组的最后一位下标n-1，此时记录结果
        if(x == n) {
            String s = String.valueOf(num).substring(start);   //从start开始截取字符串，如"01"截取后就是"1"
            if(!s.equals("0")) res[count++] = Integer.parseInt(s);   //防止将"0"、"00"、"000"加进来
            if(n - start == nine) start--;   //n减去start等于nine，表示要进位了，进位就是将左边界start左移一位，即-1
            return;
        }
        //给char数组第x位添加数字，添加完后进入下一位
        for(char i : loop) {
            if(i == '9') nine++;
            num[x] = i;
            dfs(x + 1);
        }
        nine--;   //回溯
    }
}