leetcode——树

Posted on 2022-05-01 Edited on 2023-02-24 In Java Word count in article: 49k Reading time ≈ 45 mins.

前言

记录一下leetcode树部分题目的刷题笔记

一、二叉树的深度优先遍历

前序遍历
中序遍历
后序遍历

这三种遍历方式，我个人比较倾向于递归法来实现，因为递归法的代码简洁，三种遍历的写法很类似。

其实还可以使用统一迭代法来实现这三种遍历方式，但个人觉得还是有点难记~可以当作扩展来了解

94. 二叉树的中序遍历

给定一个二叉树的根节点 root ，返回 它的中序遍历 。
1
2
输入：root = [1,null,2,3]
输出：[1,3,2]

思路：递归

首先我们需要了解什么是二叉树的中序遍历：按照访问左子树——根节点——右子树的方式遍历这棵树，而在访问左子树或者右子树的时候我们按照同样的方式遍历，直到遍历完整棵树。因此整个遍历过程天然具有递归的性质，我们可以直接用递归函数来模拟这一过程。

定义 inorder(root) 表示当前遍历到 root 节点的答案，那么按照定义，我们只要递归调用 inorder(root.left) 来遍历 root 节点的左子树，然后将 root 节点的值加入答案，再递归调用inorder(root.right) 来遍历 root 节点的右子树即可，递归终止的条件为碰到空节点。

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public List<Integer> inorderTraversal(TreeNode root) {
        List<Integer> nums = new ArrayList<Integer>();
        inorder(root,nums);
        return nums;
    }

    public void inorder(TreeNode root , List<Integer> res){
        if(root != null){
            inorder(root.left,res);
            res.add(root.val);
            inorder(root.right,res);
        }
    }
}

执行用时：0 ms, 在所有 Java 提交中击败了100.00%的用户
内存消耗：39.7 MB, 在所有 Java 提交中击败了21.80%的用户
通过测试用例：70 / 70

144. 二叉树的前序遍历

给你二叉树的根节点 root ，返回它节点值的前序遍历。

例1：
1
2
输入：root = [1,null,2,3]
输出：[1,2,3]

思路：递归

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public List<Integer> preorderTraversal(TreeNode root) {
        List<Integer> ans = new ArrayList<Integer>();
        inorder(root,ans);
        return ans;
    }

    public void inorder(TreeNode root,List<Integer> ans){
        if(root != null){
            ans.add(root.val);
            inorder(root.left,ans);
            inorder(root.right,ans);
        }
    }
}

145. 二叉树的后序遍历

思路：递归

还是和前面两题一样，二叉树的三种递归遍历写法都是一样的，只是有略微的改变而已

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public List<Integer> postorderTraversal(TreeNode root) {
        List<Integer> ans = new ArrayList<Integer>();
        inorder(root , ans);
        return ans;
    }

    public void inorder(TreeNode root , List<Integer> ans){
        if(root != null){
            inorder(root.left, ans);
            inorder(root.right , ans);
            ans.add(root.val);
        }
    }
}

二、二叉树的广度优先遍历（层序遍历）

接下来的例题是二叉树的另一种遍历方式：层序遍历。

层序遍历一个二叉树。就是从左到右一层一层的去遍历二叉树。这种遍历的方式和之前的深度优先遍历都不太一样。

需要借用一个辅助数据结构即队列来实现，队列先进先出，符合一层一层遍历的逻辑，而是用栈先进后出适合模拟深度优先遍历也就是递归的逻辑。

而这种层序遍历方式就是图论中的广度优先遍历，只不过我们应用在二叉树上。

102. 二叉树的层序遍历

给你二叉树的根节点 root ，返回其节点值的 层序遍历 。（即逐层地，从左到右访问所有节点）

示例 1:
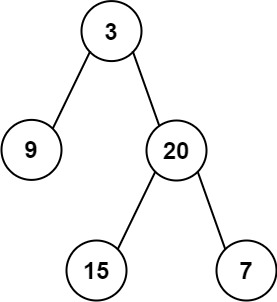
1
2
输入：root = [3,9,20,null,null,15,7]
输出：[[3],[9,20],[15,7]]

思路1：迭代+队列

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public List<List<Integer>> resList = new ArrayList<List<Integer>>();

    public List<List<Integer>> levelOrder(TreeNode root) {
        checkFun(root);
        return resList; 
    }

    public void checkFun(TreeNode node){
        if(node == null) return ;
        Queue<TreeNode> que = new LinkedList<TreeNode>();
        que.offer(node);

        while(!que.isEmpty()){
            int len = que.size();
            List<Integer> item = new ArrayList<Integer>();

            while(len > 0 ){
                TreeNode tempNode = que.poll();
                item.add(tempNode.val);

                if(tempNode.left != null){
                    que.offer(tempNode.left);
                }
                if(tempNode.right != null){
                    que.offer(tempNode.right);
                }

                len--;
            }
            resList.add(item);
        }
    }
}

思路2：递归

class Solution {
    public List<List<Integer>> resList = new ArrayList<List<Integer>>();

    public List<List<Integer>> levelOrder(TreeNode root) {
        checkFun01(root,0);
        return resList;
    }

    //DFS--递归方式
    public void checkFun01(TreeNode node, Integer deep) {
        if (node == null) return;
        deep++;

        if (resList.size() < deep) {
            //当层级增加时，list的Item也增加，利用list的索引值进行层级界定
            List<Integer> item = new ArrayList<Integer>();
            resList.add(item);
        }
        resList.get(deep - 1).add(node.val);

        checkFun01(node.left, deep);
        checkFun01(node.right, deep);
    }
}

107. 二叉树的层序遍历 II

给你二叉树的根节点 root ，返回其节点值 自底向上的层序遍历 。（即按从叶子节点所在层到根节点所在的层，逐层从左向右遍历）
1
2
输入：root = [3,9,20,null,null,15,7]
输出：[[15,7],[9,20],[3]]

思路：递归+列表翻转

和前面一题同样解法，只不过加上了一个列表反转。这里采用的是递归，因为发现递归似乎更快一些~

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public List<List<Integer>> resList = new ArrayList<List<Integer>>();

    public List<List<Integer>> levelOrderBottom(TreeNode root) {
        checkFun(root,0);
        Collections.reverse(resList);
        return resList;
    }

    public void checkFun(TreeNode node , int deep){
        if(node == null) return ;
        deep++;

        if(resList.size() < deep){
            List<Integer> item = new ArrayList<Integer>();
            resList.add(item);
        }
        resList.get(deep-1).add(node.val);

        checkFun(node.left,deep);
        checkFun(node.right,deep);
    }
}

199. 二叉树的右视图

给定一个二叉树的 根节点 root，想象自己站在它的右侧，按照从顶部到底部的顺序，返回从右侧所能看到的节点值。

思路：广度优先搜索

先获取广度优先结果，再将广度优先结果中每层的最后一个元素（也就是右视图）保留下来。

这里实现主体还是用的前面的递归，想法似乎有点复杂

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public List<Integer> resList = new ArrayList<Integer>();

    public List<Integer> rightSideView(TreeNode root) {
        checkFun(root,0);
        return resList;
    }

    public void checkFun(TreeNode node , int deep){
        if(node == null) return ;
        deep++;

        if(resList.size() < deep){
            resList.add(node.val);
        }
        if(node.right != null){
            checkFun(node.right,deep);
        }else{
            checkFun(node.left,deep);
        }
    }
}

637. 二叉树的层平均值

给定一个非空二叉树的根节点 root , 以数组的形式返回每一层节点的平均值。与实际答案相差 10-5 以内的答案可以被接受
1
2
3
4
输入：root = [3,9,20,null,null,15,7]
输出：[3.00000,14.50000,11.00000]
解释：第 0 层的平均值为 3,第 1 层的平均值为 14.5,第 2 层的平均值为 11 。
因此返回 [3, 14.5, 11] 。

思路：层序遍历

一开始的递归写法：

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public List<List<Integer>> tempList = new ArrayList<List<Integer>>();
    public List<Double> resList = new ArrayList<Double>();

    public List<Double> averageOfLevels(TreeNode root) {
        checkFun(root,0);
        for(int i =  0 ; i < tempList.size() ; i++){
            List<Integer> Lists = tempList.get(i);
            Double sum = 0.0 ;
            for(int j = 0 ; j < Lists.size();j++){
                sum += (double)(Lists.get(j));
            }
            Double ave = (sum/Lists.size());
            resList.add(ave);
        }
        return resList;
    }

    public void checkFun(TreeNode node , int deep){
        if(node == null) return ;
        deep++;

        if(tempList.size() < deep){
            List<Integer> item = new ArrayList<Integer>();
            tempList.add(item);
        }
        tempList.get(deep-1).add(node.val);

        checkFun(node.left , deep);
        checkFun(node.right , deep);
    }
}

迭代写法：

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public List<Double> averageOfLevels(TreeNode root) {
        List<Double> averages = new ArrayList<Double>();
        Queue<TreeNode> queue = new LinkedList<TreeNode>();
        queue.offer(root);
        while(!queue.isEmpty()){
            double sum = 0 ;
            int size = queue.size();
            for(int i = 0 ; i < size; i++){
                TreeNode node = queue.poll();
                sum += node.val;
                TreeNode left =node.left , right = node.right;
                if(left != null){
                    queue.offer(left);
                }
                if(right != null){
                    queue.offer(right);
                }
            }
            averages.add(sum/size);
        }
        return averages;
    }
}

429. N 叉树的层序遍历

给定一个 N 叉树，返回其节点值的层序遍历。（即从左到右，逐层遍历）。

树的序列化输入是用层序遍历，每组子节点都由 null 值分隔（参见示例）

思路：层序遍历

这里用的是迭代的写法：

/*
// Definition for a Node.
class Node {
    public int val;
    public List<Node> children;

    public Node() {}

    public Node(int _val) {
        val = _val;
    }

    public Node(int _val, List<Node> _children) {
        val = _val;
        children = _children;
    }
};
*/

class Solution {
    public List<List<Integer>> levelOrder(Node root) {
        if(root == null)    return new ArrayList<List<Integer>>();

        List<List<Integer>> ans = new ArrayList<List<Integer>>();
        Queue<Node> queue = new ArrayDeque<Node>();
        queue.offer(root);

        while(!queue.isEmpty()){
            int count = queue.size();
            List<Integer> item = new ArrayList<Integer>();
            for(int i = 0 ; i < count ; i++){
                Node cur = queue.poll();
                item.add(cur.val);
                for(Node child : cur.children){
                    queue.offer(child);
                }
            }
            ans.add(item);
        } 
        return ans;
    }
}

515. 在每个树行中找最大值

给定一棵二叉树的根节点 root ，请找出该二叉树中每一层的最大值。

示例1：

输入: root = [1,3,2,5,3,null,9]
输出: [1,3,9]

思路：广度优先搜索

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public List<Integer> largestValues(TreeNode root) {
        if(root == null)    return new ArrayList<Integer>();

        Queue<TreeNode> queue = new ArrayDeque<TreeNode>();
        List<Integer> ans = new ArrayList<Integer>();
        queue.offer(root);

        while(!queue.isEmpty()){
            int count = queue.size();
            int max = Integer.MIN_VALUE;//负数也是可以的
            for(int i = 0 ; i < count ; i++){
                TreeNode cur = queue.poll(); 
                max = cur.val > max?cur.val :max;
                TreeNode left = cur.left , right = cur.right;
                if(left != null)    queue.offer(left);
                if(right != null)   queue.offer(right);
            }
            ans.add(max);
        }
        return ans;
    }
}

116. 填充每个节点的下一个右侧节点指针

给定一个完美二叉树，其所有叶子节点都在同一层，每个父节点都有两个子节点。二叉树定义如下：

struct Node {
int val;
Node *left;
Node *right;
Node *next;
}
填充它的每个 next 指针，让这个指针指向其下一个右侧节点。如果找不到下一个右侧节点，则将 next 指针设置为 NULL。

初始状态下，所有 next 指针都被设置为 NULL。

示例 1：

输入：root = [1,2,3,4,5,6,7]
输出：[1,#,2,3,#,4,5,6,7,#]
解释：给定二叉树如图 A 所示，你的函数应该填充它的每个 next 指针，以指向其下一个右侧节点，如图 B 所示。序列化的输出按层序遍历排列，同一层节点由 next 指针连接，’#’ 标志着每一层的结束。

思路：广度优先搜索

/*
// Definition for a Node.
class Node {
    public int val;
    public Node left;
    public Node right;
    public Node next;

    public Node() {}
    
    public Node(int _val) {
        val = _val;
    }

    public Node(int _val, Node _left, Node _right, Node _next) {
        val = _val;
        left = _left;
        right = _right;
        next = _next;
    }
};
*/

class Solution {
    public Node connect(Node root) {
        if(root == null)    return root;
        Queue<Node> queue = new ArrayDeque<Node>();
        queue.offer(root);

        while(!queue.isEmpty()){
            int count = queue.size();
            for(int i = 0 ; i < count ; i++){
                Node cur = queue.poll();
                if(i < count -1){
                    cur.next = queue.peek();
                }
                if(cur.left != null)    queue.offer(cur.left);    
                if(cur.right != null)    queue.offer(cur.right);
            }
        }
        return root;
    }
}

104. 二叉树的最大深度

给定一个二叉树，找出其最大深度。

二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。

说明: 叶子节点是指没有子节点的节点。

思路1：广度优先搜索

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public int maxDepth(TreeNode root) {
        if(root == null) return 0;

        Queue<TreeNode> queue = new ArrayDeque<TreeNode>();
        queue.offer(root);
        int ans = 0;

        while(!queue.isEmpty()){
            int count = queue.size();
            for(int i = 0 ; i < count ; i++){
                TreeNode cur = queue.poll();
                if(cur.left != null){
                    queue.offer(cur.left);
                }
                if(cur.right != null){
                    queue.offer(cur.right);
                }
            }
            ans++;
        }
        return ans;
    }
}

思路2：深度优先搜索

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public int maxDepth(TreeNode root) {
        if(root == null){
            return 0;
        }else{
            int leftHeight = maxDepth(root.left);
            int rightHeight = maxDepth(root.right);
            return Math.max(leftHeight,rightHeight)+1;
        }
    }
}

111. 二叉树的最小深度

给定一个二叉树，找出其最小深度。

最小深度是从根节点到最近叶子节点的最短路径上的节点数量。

说明：叶子节点是指没有子节点的节点。

示例 1：

输入：root = [3,9,20,null,null,15,7]
输出：2

思路1：广度优先搜索

class Solution {
    class QueueNode {
        TreeNode node;
        int depth;

        public QueueNode(TreeNode node, int depth) {
            this.node = node;
            this.depth = depth;
        }
    }

    public int minDepth(TreeNode root) {
        if (root == null) {
            return 0;
        }

        Queue<QueueNode> queue = new LinkedList<QueueNode>();
        queue.offer(new QueueNode(root, 1));
        while (!queue.isEmpty()) {
            QueueNode nodeDepth = queue.poll();
            TreeNode node = nodeDepth.node;
            int depth = nodeDepth.depth;
            if (node.left == null && node.right == null) {
                return depth;
            }
            if (node.left != null) {
                queue.offer(new QueueNode(node.left, depth + 1));
            }
            if (node.right != null) {
                queue.offer(new QueueNode(node.right, depth + 1));
            }
        }

        return 0;
    }
}

思路2：深度优先搜索

class Solution {
    public int minDepth(TreeNode root) {
        if (root == null) {
            return 0;
        }

        if (root.left == null && root.right == null) {
            return 1;
        }

        int min_depth = Integer.MAX_VALUE;
        if (root.left != null) {
            min_depth = Math.min(minDepth(root.left), min_depth);
        }
        if (root.right != null) {
            min_depth = Math.min(minDepth(root.right), min_depth);
        }

        return min_depth + 1;
    }
}

三、翻转二叉树

226. 翻转二叉树

给你一棵二叉树的根节点 root ，翻转这棵二叉树，并返回其根节点。
1
2
输入：root = [4,2,7,1,3,6,9]
输出：[4,7,2,9,6,3,1]

思路：深度优先搜索（递归）

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public TreeNode invertTree(TreeNode root) {
        if(root == null) return root;
        TreeNode left = root.left , right = root.right;
        TreeNode temp = left;
        root.left = right;
        root.right = temp;
        invertTree(left);
        invertTree(right);
        return root;
    }
}

四、对称二叉树

101. 对称二叉树

给你一个二叉树的根节点 root ，检查它是否轴对称。
1
2
输入：root = [1,2,2,3,4,4,3]
输出：true

思路：递归

对于二叉树是否对称，要比较的是根节点的左子树与右子树是不是相互翻转的，理解这一点就知道了其实我们要比较的是两个树（这两个树是根节点的左右子树），所以在递归遍历的过程中，也是要同时遍历两棵树。所以比较的是两个子树的里侧和外侧的元素是否相等。

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public boolean isSymmetric(TreeNode root) {
        return compare(root.left,root.right);
    }

    public boolean compare(TreeNode left , TreeNode right){
        if(left == null && right == null)   return true;
        if(left !=null && right == null) return false;
        if(left == null && right != null) return false;
        if(left.val != right.val)   return false;
        boolean compareOutside = compare(left.left , right.right);
        boolean compareInside = compare(left.right , right.left);
        return compareOutside&&compareInside;
    }
}

100. 相同的树

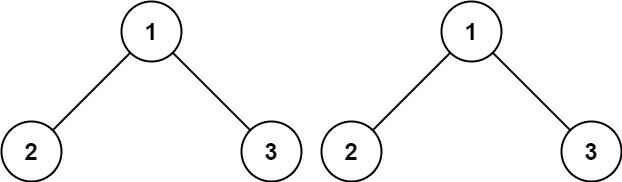
给你两棵二叉树的根节点 p 和 q ，编写一个函数来检验这两棵树是否相同。

如果两个树在结构上相同，并且节点具有相同的值，则认为它们是相同的。
1
2
输入：p = [1,2,3], q = [1,2,3]
输出：true

五、完全二叉树的节点个数

222. 完全二叉树的节点个数

给你一棵完全二叉树的根节点 root ，求出该树的节点个数。

完全二叉树的定义如下：在完全二叉树中，除了最底层节点可能没填满外，其余每层节点数都达到最大值，并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层，则该层包含 1~ 2h 个节点。
1
2
输入：root = [1,2,3,4,5,6]
输出：6

思路：递归

首先需要明确完全二叉树的定义：它是一棵空树或者它的叶子节点只出在最后两层，若最后一层不满则叶子节点只在最左侧

再来回顾一下满二叉的节点个数怎么计算，如果满二叉树的层数为h，则总节点数为：2^h - 1.
那么我们来对 root 节点的左右子树进行高度统计，分别记为 left 和 right，有以下两种结果：

left == right。这说明，左子树一定是满二叉树，因为节点已经填充到右子树了，左子树必定已经填满了。所以左子树的节点总数我们可以直接得到，是 2^left - 1，加上当前这个 root 节点，则正好是 2^left。再对右子树进行递归统计。
left != right。说明此时最后一层不满，但倒数第二层已经满了，可以直接得到右子树的节点个数。同理，右子树节点 +root 节点，总数为 2^right。再对左子树进行递归查找。

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public int countNodes(TreeNode root) {
        if(root == null) return 0;
        int left = countLevel(root.left);
        int right = countLevel(root.right);
        if(left == right){
            return countNodes(root.right)+(1<<left);
        }else{
            return countNodes(root.left)+(1<<right);
        }
    }

    public int countLevel(TreeNode root){
        int level = 0 ;
        while(root != null){
            level++;
            root = root.left;
        }
        return level;
    }
}

六、平衡二叉树

110. 平衡二叉树

给定一个二叉树，判断它是否是高度平衡的二叉树。

本题中，一棵高度平衡二叉树定义为：

一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过 1 。
1
2
输入：root = [3,9,20,null,null,15,7]
输出：true

思路：递归

class Solution {
    public boolean isBalanced(TreeNode root) {
        if(root == null){
            return true;
        }
        else{
            return Math.abs(height(root.left)-height(root.right)) <=1 && isBalanced(root.left) && isBalanced(root.right);
        }   
    }

    public int height(TreeNode node){
        if(node == null){
            return 0;
        }else{
            return Math.max(height(node.left),height(node.right))+1;
        }
    }
}

七、二叉树的所有路径

257. 二叉树的所有路径

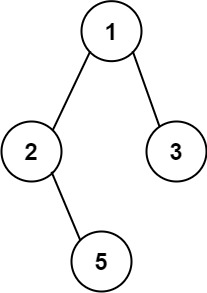
给你一个二叉树的根节点 root ，按 任意顺序 ，返回所有从根节点到叶子节点的路径。

叶子节点 是指没有子节点的节点。
1
2
输入：root = [1,2,3,null,5]
输出：["1->2->5","1->3"]

思路1：深度优先搜索（递归）

如果当前节点不是叶子节点，则在当前的路径末尾添加该节点，并继续递归遍历该节点的每一个孩子节点。
如果当前节点是叶子节点，则在当前路径末尾添加该节点后我们就得到了一条从根节点到叶子节点的路径，将该路径加入到答案即可。

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public List<String> binaryTreePaths(TreeNode root) {
        List<String> paths = new ArrayList<String>();
        constructPaths(root,"",paths);
        return paths;
    }

    public void constructPaths(TreeNode root,String path,List<String>paths){
        if(root != null){
            StringBuffer pathSB = new StringBuffer(path);
            pathSB.append(Integer.toString(root.val));
            if(root.left == null && root.right == null){
                paths.add(pathSB.toString());
            }else{
                pathSB.append("->");
                constructPaths(root.left,pathSB.toString(),paths);
                constructPaths(root.right,pathSB.toString(),paths);
            }
        }
    }
}

时间复杂度：O(N^2)
空间复杂度：O(N^2)

思路2：广度优先搜索

我们也可以用广度优先搜索来实现。我们维护一个队列，存储节点以及根到该节点的路径。一开始这个队列里只有根节点。在每一步迭代中，我们取出队列中的首节点，如果它是叶子节点，则将它对应的路径加入到答案中。如果它不是叶子节点，则将它的所有孩子节点加入到队列的末尾。当队列为空时广度优先搜索结束，我们即能得到答案。

class Solution {
    public List<String> binaryTreePaths(TreeNode root) {
        List<String> paths = new ArrayList<String>();
        if (root == null) {
            return paths;
        }
        Queue<TreeNode> nodeQueue = new LinkedList<TreeNode>();
        Queue<String> pathQueue = new LinkedList<String>();

        nodeQueue.offer(root);
        pathQueue.offer(Integer.toString(root.val));

        while (!nodeQueue.isEmpty()) {
            TreeNode node = nodeQueue.poll(); 
            String path = pathQueue.poll();

            if (node.left == null && node.right == null) {
                paths.add(path);
            } else {
                if (node.left != null) {
                    nodeQueue.offer(node.left);
                    pathQueue.offer(new StringBuffer(path).append("->").append(node.left.val).toString());
                }

                if (node.right != null) {
                    nodeQueue.offer(node.right);
                    pathQueue.offer(new StringBuffer(path).append("->").append(node.right.val).toString());
                }
            }
        }
        return paths;

八、左叶子之和

404. 左叶子之和

给定二叉树的根节点 root ，返回所有左叶子之和

输入: root = [3,9,20,null,null,15,7]
输出: 24
解释: 在这个二叉树中，有两个左叶子，分别是 9 和 15，所以返回 24

思路1：深度优先搜索

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public int sumOfLeftLeaves(TreeNode root) {
        return root != null ? dfs(root):0;
    }

    public int dfs(TreeNode node){
        int ans = 0;
        if(node.left != null){
            ans += isLeafNode(node.left) ? node.left.val : dfs(node.left);
        }
        if(node.right != null && !isLeafNode(node.right)){
            ans += dfs(node.right);
        }
        return ans;
    }
    public boolean isLeafNode(TreeNode node){
        return node.left ==null && node.right == null;
    }
}

思路2：广度优先搜索

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public int sumOfLeftLeaves(TreeNode root) {
        if(root == null)    return 0;

        Queue<TreeNode> queue = new LinkedList<TreeNode>();
        queue.offer(root);
        int ans = 0;

        while(!queue.isEmpty()){
            TreeNode node = queue.poll();
            if(node.left != null){
                if(isLeafNode(node.left)){
                    ans += node.left.val;
                }else{
                    queue.offer(node.left);
                }
            }
            if(node.right != null){
                if(!isLeafNode(node.right)){
                    queue.offer(node.right);
                }
            }
        }
        return ans;
    }

    public boolean isLeafNode(TreeNode node){
        return node.left == null && node.right==null;
    }
}

九、找树左下角的值

513. 找树左下角的值

给定一个二叉树的 根节点 root，请找出该二叉树的 最底层最左边 节点的值。

假设二叉树中至少有一个节点。
1
2
输入: root = [2,1,3]
输出: 1

思路1：广度优先搜索

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public int findBottomLeftValue(TreeNode root) {
        if(root == null) return 0;

        List<List<Integer>> list = new ArrayList<List<Integer>>();
        Queue<TreeNode> queue = new LinkedList<TreeNode>();
        queue.offer(root);

        while(!queue.isEmpty()){
            int len = queue.size();
            List<Integer> item = new ArrayList<Integer>();
            while(len > 0){
                TreeNode temp = queue.poll();
                item.add(temp.val);

                if(temp.left != null){
                    queue.offer(temp.left);
                }
                if(temp.right != null){
                    queue.offer(temp.right);
                }
                len--;
            }
            list.add(item);
        }
        List last = list.get(list.size()-1);
        return (int)last.get(0);
    }
}

附上优化后的广度优先搜索：

题目要求输出最底层最左的元素，我们只需要先序广度搜索这棵树，并把元素分别入队出队，最后出队的那个就是那个最底层最左的元素了

public int findBottomLeftValue(TreeNode root) {
        Deque<TreeNode> deque = new LinkedList<>();
        deque.offer(root);
        TreeNode poll = null;
        while (!deque.isEmpty()){
            poll = deque.poll();
            if (poll.right != null){
                deque.offer(poll.right);
            }
            if (poll.left != null){
                deque.offer(poll.left);
            }
        }
        return poll.val;
    }

十、路径总和

112. 路径总和

给你二叉树的根节点 root 和一个表示目标和的整数 targetSum 。判断该树中是否存在根节点到叶子节点的路径，这条路径上所有节点值相加等于目标和 targetSum 。如果存在，返回 true ；否则，返回 false 。

叶子节点是指没有子节点的节点。

输入：root = [5,4,8,11,null,13,4,7,2,null,null,null,1], targetSum = 22
输出：true
解释：等于目标和的根节点到叶节点路径如上图所示。

思路：广度优先搜索

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public boolean hasPathSum(TreeNode root, int targetSum) {
        if(root == null)    return false;

        Queue<TreeNode> queueNode = new LinkedList<TreeNode>();
        Queue<Integer> queueVal = new LinkedList<Integer>();
        queueNode.offer(root);
        queueVal.offer(root.val);
        
        while(!queueNode.isEmpty()){
            TreeNode currNode = queueNode.poll();
            int temp = queueVal.poll();
            if(currNode.left == null && currNode.right ==null){
                if(temp == targetSum){
                    return true;
                }
                continue;
            }
            if(currNode.left != null){
                queueNode.offer(currNode.left);
                queueVal.offer(temp + currNode.left.val);
            }
            if(currNode.right != null){
                queueNode.offer(currNode.right);
                queueVal.offer(temp + currNode.right.val);
            }
        }
        return false;
    }
}

113. 路径总和 II

给你二叉树的根节点 root 和一个整数目标和 targetSum ，找出所有从根节点到叶子节点路径总和等于给定目标和的路径。

叶子节点是指没有子节点的节点。

输入：root = [5,4,8,11,null,13,4,7,2,null,null,5,1], targetSum = 22
输出：[[5,4,11,2],[5,8,4,5]]

思路：深度优先搜索（回溯）

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public List<List<Integer>> pathSum(TreeNode root, int targetSum) {
        List<List<Integer>> res = new ArrayList<List<Integer>>();
        if(root == null) return res;

        List<Integer>  path = new ArrayList<Integer>();
        dfs(root,targetSum,res,path);
        return res;
    }

    public void dfs(TreeNode root , int targetSum , List<List<Integer>> res,List<Integer>path){
        path.add(root.val);
        //遇到了叶子节点
        if(root.left == null && root.right == null){
            //找到了和为targetSum的路径
            if(targetSum - root.val == 0){
                res.add(new ArrayList<Integer>(path));
            }
            return ;//如果和补位targetsum，直接返回
        }
        if(root.left != null){
            dfs(root.left , targetSum - root.val , res , path);
            path.remove(path.size()-1);//回溯
        }
        if(root.right != null){
            dfs(root.right , targetSum - root.val , res , path);
            path.remove(path.size()-1);//回溯
        }
    }
}

十一、从中序与后序遍历序列构造二叉树

106. 从中序与后序遍历序列构造二叉树

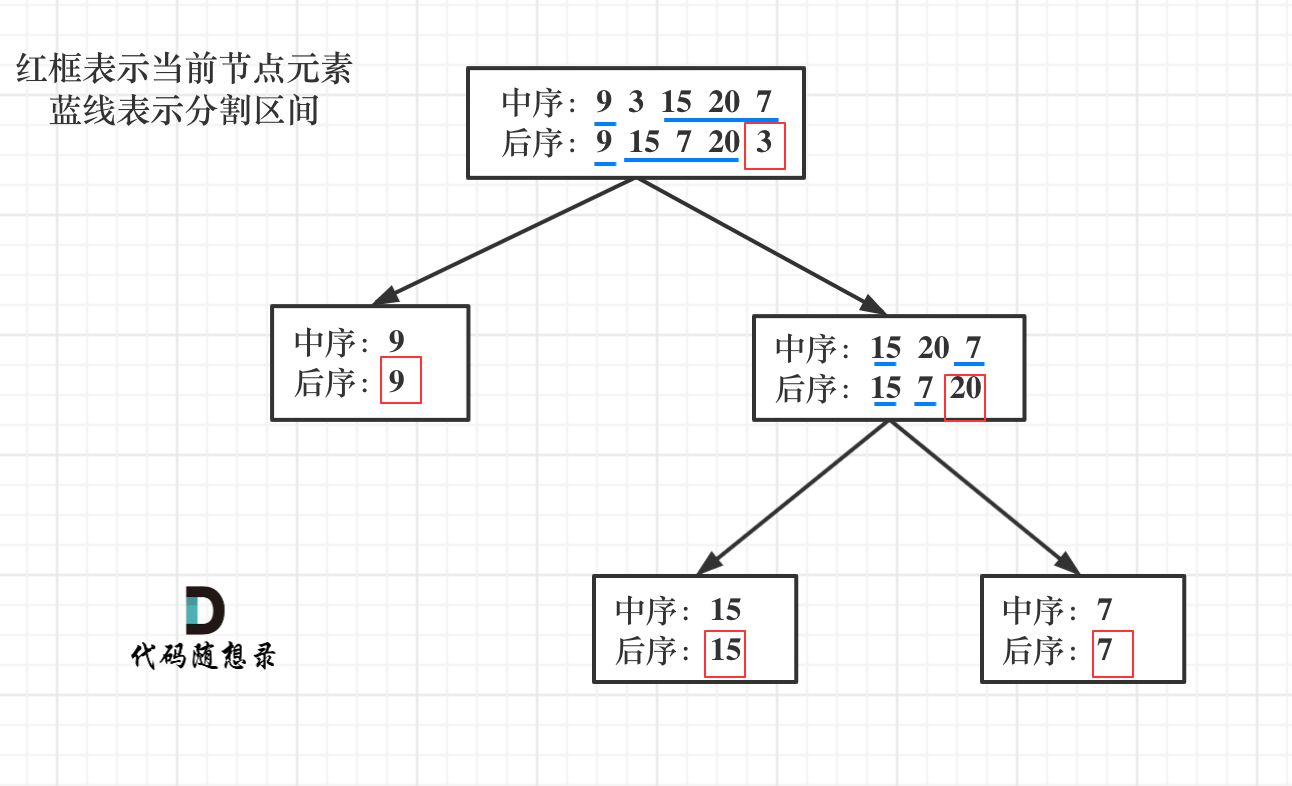
给定两个整数数组 inorder 和 postorder ，其中 inorder 是二叉树的中序遍历， postorder 是同一棵树的后序遍历，请你构造并返回这颗二叉树。

输入：inorder = [9,3,15,20,7], postorder = [9,15,7,20,3]
输出：[3,9,20,null,null,15,7]

思路：递归

说到一层一层切割，就应该想到了递归。

来看一下一共分几步：

第一步：如果数组大小为零的话，说明是空节点了。
第二步：如果不为空，那么取后序数组最后一个元素作为节点元素。
第三步：找到后序数组最后一个元素在中序数组的位置，作为切割点
第四步：切割中序数组，切成中序左数组和中序右数组（顺序别搞反了，一定是先切中序数组）
第五步：切割后序数组，切成后序左数组和后序右数组
第六步：递归处理左区间和右区间

class Solution {
    public TreeNode buildTree(int[] inorder, int[] postorder) {
        return buildTree1(inorder,0,inorder.length,postorder,0,postorder.length);
    }
    public TreeNode buildTree1(int[] inorder , int inLeft , int inRight,int[] postorder , int postLeft , int postRight ){
        if(inRight - inLeft < 1) return null;
        if(inRight - inLeft == 1 ) return new TreeNode(inorder[inLeft]);

        int rootVal = postorder[postRight - 1 ];
        TreeNode root = new TreeNode(rootVal);
        int rootIndex = 0;

        for(int i = inLeft ; i < inRight ; i++){
            if(inorder[i] == rootVal){
                rootIndex = i ;
                break;
            }
        }

        root.left = buildTree1(inorder , inLeft , rootIndex , postorder , postLeft , postLeft+(rootIndex - inLeft));
        root.right = buildTree1(inorder , rootIndex+1 , inRight , postorder , postLeft+(rootIndex - inLeft),postRight-1);

        return root; 
    }
}

105. 从前序与中序遍历序列构造二叉树

给定两个整数数组 preorder 和 inorder ，其中 preorder 是二叉树的先序遍历， inorder 是同一棵树的中序遍历，请构造二叉树并返回其根节点

输入: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
输出: [3,9,20,null,null,15,7]

思路：递归

class Solution {
    public TreeNode buildTree(int[] preorder, int[] inorder) {
        return buildTree1(preorder,0,preorder.length-1,inorder,0,inorder.length-1);
    }

    public TreeNode buildTree1(int[] preorder , int preLeft , int preRight,int[] inorder,int inLeft,int inRight){
        if(inLeft > inRight || preLeft > preRight) return null;

        int rootVal = preorder[preLeft] , rootIndex = inLeft;
        TreeNode root = new TreeNode(rootVal);
        for(int i = inLeft ; i <= inRight ; i++){
            if(inorder[i] == rootVal){
                rootIndex = i;
                break;
            }
        }

        root.left = buildTree1(preorder,preLeft+1,preLeft+(rootIndex - inLeft),inorder,inLeft,rootIndex-1);
        root.right = buildTree1(preorder,preLeft+(rootIndex - inLeft)+1,preRight,inorder,rootIndex+1,inRight);

        return root;
    }
}

总结

前序和中序可以唯一确定一棵二叉树。

后序和中序可以唯一确定一棵二叉树。

那么前序和后序可不可以唯一确定一棵二叉树呢？

前序和后序不能唯一确定一棵二叉树！，因为没有中序遍历无法确定左右部分，也就是无法分割。

十二、最大二叉树

654. 最大二叉树

给定一个不重复的整数数组 nums 。最大二叉树可以用下面的算法从 nums 递归地构建:

创建一个根节点，其值为 nums 中的最大值。

递归地在最大值左边的子数组前缀上构建左子树。

递归地在最大值右边的子数组后缀上构建右子树。

返回 nums 构建的最大二叉树。

思路：递归

创建方法 construct(nums, l, r)，用于找出在数组 numsnums 中从 l 到 r 索引（不包含第 r 个位置）中最大二叉树的根节点。

算法步骤如下：

首先调用 construct(nums, 0, n)，其中 n 是数组 nums 的长度。
在索引范围 (l:r-1)内找到最大值的索引，将 nums[max_i]作为根节点。
调用 construct(nums, l, max_i) 创建根节点的左孩子。递归执行此操作，创建根节点的整个左子树。
类似的，调用 construct(nums, max_i + 1, r) 创建根节点的右子树。
方法 construct(nums, 0, n) 返回最大二叉树的根节点。

class Solution {
    public TreeNode constructMaximumBinaryTree(int[] nums) {
        return construct(nums,0,nums.length);
    }

    public TreeNode construct(int[] nums,int left , int right){
        if(left == right){
            return null;
        }
        int maxVal = max(nums,left,right);
        TreeNode root = new TreeNode(nums[maxVal]);
        root.left = construct(nums,left,maxVal);
        root.right = construct(nums,maxVal+1,right);
        return root;
    }

    public int max(int[] nums, int left , int right){
        int maxVal = left;
        for(int i = left ; i < right;i++){
            if(nums[maxVal] < nums[i]){
                maxVal = i;
            }
        }
        return maxVal;
    }
}

十三、合并二叉树

617. 合并二叉树

给你两棵二叉树： root1 和 root2 。

想象一下，当你将其中一棵覆盖到另一棵之上时，两棵树上的一些节点将会重叠（而另一些不会）。你需要将这两棵树合并成一棵新二叉树。合并的规则是：如果两个节点重叠，那么将这两个节点的值相加作为合并后节点的新值；否则，不为 null 的节点将直接作为新二叉树的节点。

返回合并后的二叉树。

注意: 合并过程必须从两个树的根节点开始。
1
2
输入：root1 = [1,3,2,5], root2 = [2,1,3,null,4,null,7]
输出：[3,4,5,5,4,null,7]

思路：深度优先搜索

class Solution {
    public TreeNode mergeTrees(TreeNode root1, TreeNode root2) {
        if(root1 == null){
            return root2;
        }
        if(root2 == null){
            return root1;
        }
        TreeNode merged = new TreeNode(root1.val+root2.val);
        merged.left = mergeTrees(root1.left,root2.left);
        merged.right = mergeTrees(root1.right,root2.right);
        return merged;
    }
}

十四、二叉树搜索树

700. 二叉搜索树中的搜索

给定二叉搜索树（BST）的根节点 root 和一个整数值 val。

你需要在 BST 中找到节点值等于 val 的节点。返回以该节点为根的子树。如果节点不存在，则返回 null 。
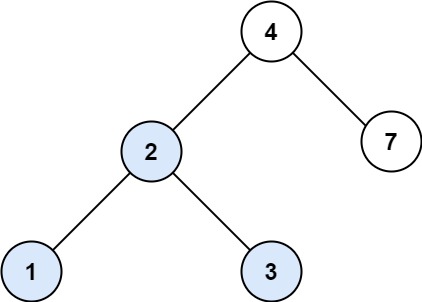
1
2
输入：root = [4,2,7,1,3], val = 2
输出：[2,1,3]

思路：递归

二叉搜索树满足如下性质：

左子树所有节点的元素值均小于根的元素值；
右子树所有节点的元素值均大于根的元素值。

据此可以得到如下算法：

若 root 为空则返回空节点；
若 val=root.val，则返回 root；
若val<root.val，递归左子树；
若 val>root.val，递归右子树。

class Solution {
    public TreeNode searchBST(TreeNode root, int val) {
        if (root == null) {
            return null;
        }
        if (val == root.val) {
            return root;
        }
        return searchBST(val < root.val ? root.left : root.right, val);
    }
}

98. 验证二叉搜索树

给你一个二叉树的根节点 root ，判断其是否是一个有效的二叉搜索树。

有效二叉搜索树定义如下：

节点的左子树只包含小于当前节点的数。
节点的右子树只包含大于当前节点的数。
所有左子树和右子树自身必须也是二叉搜索树。

思路：中序遍历

class Solution {
    long pre = Long.MIN_VALUE;
    public boolean isValidBST(TreeNode root) {
        if(root == null)    return true;
        if(!isValidBST(root.left)){
            return false;
        }

        if(root.val <= pre){
            return false;
        }
        pre = root.val;

        return isValidBST(root.right);
    }
}

530. 二叉搜索树的最小绝对差

给你一个二叉搜索树的根节点 root ，返回 树中任意两不同节点值之间的最小差值 。

差值是一个正数，其数值等于两值之差的绝对值。

思路：递归

class Solution {
    TreeNode pre;
    int result = Integer.MAX_VALUE;
    public int getMinimumDifference(TreeNode root) {
        if(root == null)    return 0;
        traversal(root);
        return result;
    }

    public void traversal(TreeNode node){
        if(node == null)    return ;
        traversal(node.left);
        if(pre != null){
            result = Math.min(result,node.val-pre.val);
        }
        pre = node;
        traversal(node.right);
    }
}

501. 二叉搜索树中的众数

给你一个含重复值的二叉搜索树（BST）的根节点 root ，找出并返回 BST 中的所有众数（即，出现频率最高的元素）。

如果树中有不止一个众数，可以按任意顺序返回。

假定 BST 满足如下定义：

结点左子树中所含节点的值小于等于当前节点的值
结点右子树中所含节点的值大于等于当前节点的值
左子树和右子树都是二叉搜索树
1
2
输入：root = [1,null,2,2]
输出：[2]

思路：中序遍历+递归

class Solution {
    ArrayList<Integer> resList;
    int maxCount;
    int count;
    TreeNode pre;

    public int[] findMode(TreeNode root) {
        resList = new ArrayList<>();
        maxCount = 0;
        count = 0;
        pre = null;
        findMode1(root);
        int[] res = new int[resList.size()];
        for(int i = 0 ; i < resList.size(); i++){
            res[i] = resList.get(i);
        }    
        return res;
    }

    public void findMode1(TreeNode root){
        if(root == null)    return ;
        findMode1(root.left);
        int rootVal = root.val;
        if(pre == null || rootVal != pre.val){
            count = 1;
        }else{
            count++;
        }

        if(count > maxCount ){
            resList.clear();
            resList.add(rootVal);
            maxCount = count;
        }else if(count == maxCount){
            resList.add(root.val);
        }
        pre = root;

        findMode1(root.right);
    }
}

十五、二叉树的最近公共祖先

236. 二叉树的最近公共祖先

给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。

百度百科中最近公共祖先的定义为：“对于有根树 T 的两个节点 p、q，最近公共祖先表示为一个节点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”

输入：root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
输出：3
解释：节点 5 和节点 1 的最近公共祖先是节点 3 。

思路：回溯

遇到这个题目首先想的是要是能自底向上查找就好了，这样就可以找到公共祖先了。

那么二叉树如何可以自底向上查找呢？

回溯啊，二叉树回溯的过程就是从低到上。

后序遍历就是天然的回溯过程，最先处理的一定是叶子节点。

接下来就看如何判断一个节点是节点q和节点p的公共公共祖先呢。

首先最容易想到的一个情况：如果找到一个节点，发现左子树出现结点p，右子树出现节点q，或者左子树出现结点q，右子树出现节点p，那么该节点就是节点p和q的最近公共祖先。

但是很多人容易忽略一个情况，就是节点本身p(q)，它拥有一个子孙节点q(p)。

使用后序遍历，回溯的过程，就是从低向上遍历节点，一旦发现满足第一种情况的节点，就是最近公共节点了。

但是如果p或者q本身就是最近公共祖先呢？其实只需要找到一个节点是p或者q的时候，直接返回当前节点，无需继续递归子树。如果接下来的遍历中找到了后继节点满足第一种情况则修改返回值为后继节点，否则，继续返回已找到的节点即可。

class Solution {
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        if(root == null || root == p || root == q){
            return root;
        }

        TreeNode left = lowestCommonAncestor(root.left,p,q);
        TreeNode right = lowestCommonAncestor(root.right,p,q);

        if(left == null && right == null){
            return null;
        }else if(left == null && right != null){
            return right;
        }else if(left != null && right == null){
            return left;
        }else{
            return root;
        }
    }
}

十六、二叉搜索树中的插入操作

701. 二叉搜索树中的插入操作

给定二叉搜索树（BST）的根节点 root 和要插入树中的值 value ，将值插入二叉搜索树。返回插入后二叉搜索树的根节点。输入数据保证，新值和原始二叉搜索树中的任意节点值都不同。

注意，可能存在多种有效的插入方式，只要树在插入后仍保持为二叉搜索树即可。你可以返回任意有效的结果。

思路

class Solution {
    public TreeNode insertIntoBST(TreeNode root, int val) {
        if(root == null){
            return new TreeNode(val);
        }

        if(root.val < val){
            root.right = insertIntoBST(root.right,val);
        }else if(root.val > val){
            root.left = insertIntoBST(root.left,val);
        }
        return root;
    }
}

十七、删除二叉搜索树中的节点

450. 删除二叉搜索树中的节点

给定一个二叉搜索树的根节点 root 和一个值 key，删除二叉搜索树中的 key 对应的节点，并保证二叉搜索树的性质不变。返回二叉搜索树（有可能被更新）的根节点的引用。

一般来说，删除节点可分为两个步骤：

首先找到需要删除的节点；
如果找到了，删除它。

输入：root = [5,3,6,2,4,null,7], key = 3
输出：[5,4,6,2,null,null,7]
解释：给定需要删除的节点值是 3，所以我们首先找到 3 这个节点，然后删除它。
一个正确的答案是 [5,4,6,2,null,null,7], 如下图所示。
另一个正确答案是 [5,2,6,null,4,null,7]。

思路

有以下五种情况：

第一种情况：没找到删除的节点，遍历到空节点直接返回了
找到删除的节点
- 第二种情况：左右孩子都为空（叶子节点），直接删除节点，返回NULL为根节点
- 第三种情况：删除节点的左孩子为空，右孩子不为空，删除节点，右孩子补位，返回右孩子为根节点
- 第四种情况：删除节点的右孩子为空，左孩子不为空，删除节点，左孩子补位，返回左孩子为根节点
- 第五种情况：左右孩子节点都不为空，则将删除节点的左子树头结点（左孩子）放到删除节点的右子树的最左面节点的左孩子上，返回删除节点右孩子为新的根节点。

第五种情况有点难以理解，看下面动画：

class Solution {
    public TreeNode deleteNode(TreeNode root, int key) {
        root = delete(root,key);
        return root;
    }

    public TreeNode delete(TreeNode root, int key){
        if(root == null)    return null;

        if(root.val > key){
            root.left = delete(root.left,key);
        }else if(root.val < key){
            root.right = delete(root.right,key);
        }else{
            if(root.left == null) return root.right;
            if(root.right == null) return root.left;
            TreeNode tmp = root.right;
            while(tmp.left != null){
                tmp = tmp.left;
            }
            root.val = tmp.val;
            root.right = delete(root.right,tmp.val);
        }
        return root;
    }
}

十八、修剪二叉搜索树

669. 修剪二叉搜索树

给你二叉搜索树的根节点 root ，同时给定最小边界low 和最大边界 high。通过修剪二叉搜索树，使得所有节点的值在[low, high]中。修剪树不应该改变保留在树中的元素的相对结构 (即，如果没有被移除，原有的父代子代关系都应当保留)。可以证明，存在唯一的答案。

所以结果应当返回修剪好的二叉搜索树的新的根节点。注意，根节点可能会根据给定的边界发生改变。
1
2
输入：root = [1,0,2], low = 1, high = 2
输出：[1,null,2]
1
2
输入：root = [3,0,4,null,2,null,null,1], low = 1, high = 3
输出：[3,2,null,1]

思路递归

class Solution {
    public TreeNode trimBST(TreeNode root, int low, int high) {
        if(root == null){
            return null;
        }
        if(root.val < low){
            return trimBST(root.right,low,high);
        }
        if(root.val > high){
            return trimBST(root.left,low,high);
        }
        //root在[low,high]范围内，继续
        root.left = trimBST(root.left,low,high);
        root.right = trimBST(root.right,low,high);
        return root;
    }
}

十九、将有序数组转换为二叉搜索树

108. 将有序数组转换为二叉搜索树

给你一个整数数组 nums ，其中元素已经按升序排列，请你将其转换为一棵高度平衡二叉搜索树。

高度平衡二叉树是一棵满足「每个节点的左右两个子树的高度差的绝对值不超过 1 」的二叉树。

输入：nums = [-10,-3,0,5,9]
输出：[0,-3,9,-10,null,5]
解释：[0,-10,5,null,-3,null,9] 也将被视为正确答案：

思路：递归

class Solution {
    public TreeNode sortedArrayToBST(int[] nums) {
        TreeNode root = sorted(nums,0,nums.length-1);
        return root;
    }

    public TreeNode sorted(int[] nums , int left, int right){
        if(left > right) return null;

        int mid = left + ((right -left) >>1);
        TreeNode root = new TreeNode(nums[mid]);
        root.left = sorted(nums,left,mid-1);
        root.right = sorted(nums,mid+1,right);
        return root;
    }
}

二十、把二叉搜索树转换为累加树

538. 把二叉搜索树转换为累加树

给出二叉搜索树的根节点，该树的节点值各不相同，请你将其转换为累加树（Greater Sum Tree），使每个节点 node 的新值等于原树中大于或等于 node.val 的值之和。

提醒一下，二叉搜索树满足下列约束条件：

节点的左子树仅包含键小于节点键的节点。
节点的右子树仅包含键大于节点键的节点。
左右子树也必须是二叉搜索树。
注意：本题和 1038: https://leetcode-cn.com/problems/binary-search-tree-to-greater-sum-tree/ 相同

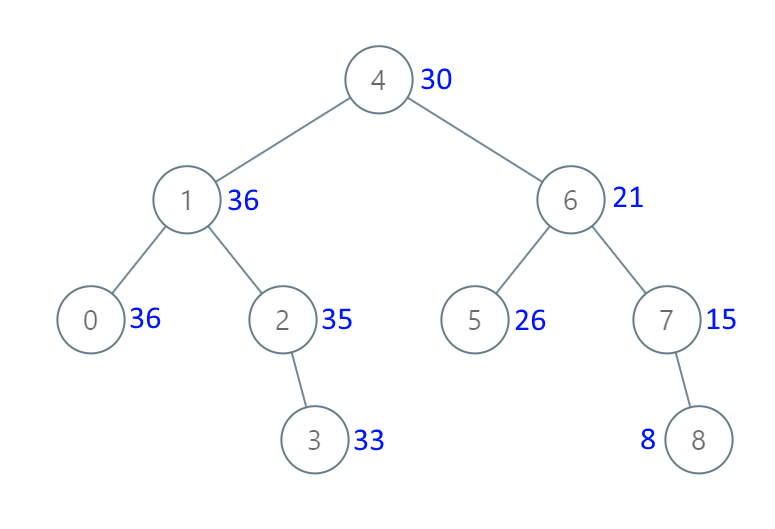
输入：[4,1,6,0,2,5,7,null,null,null,3,null,null,null,8]
输出：[30,36,21,36,35,26,15,null,null,null,33,null,null,null,8]

思路：反中序遍历

利用二叉搜索树的性质：

换一个角度来看，这就是一个有序数组[2, 5, 13]，求从后到前的累加数组，也就是[20, 18, 13]，是不是感觉这就简单了。

那么知道如何遍历这个二叉树，也就迎刃而解了，从树中可以看出累加的顺序是右中左，所以我们需要反中序遍历这个二叉树，然后顺序累加就可以了。

class Solution {
    int sum;
    public TreeNode convertBST(TreeNode root) {
        sum = 0;
        convertBST1(root);
        return root;
    }
    public void convertBST1(TreeNode root){
        if(root == null){
            return ;
        }
        convertBST1(root.right);
        sum += root.val;
        root.val = sum;
        convertBST1(root.left);
    }
}

前言

一、二叉树的深度优先遍历

思路：递归

思路：递归

思路：递归

二、二叉树的广度优先遍历（层序遍历）

思路1：迭代+队列

思路2：递归

思路：递归+列表翻转

思路：广度优先搜索

思路：层序遍历

思路：层序遍历

思路：广度优先搜索

思路：广度优先搜索

思路1：广度优先搜索

思路2：深度优先搜索

思路1：广度优先搜索

思路2：深度优先搜索

三、翻转二叉树

思路：深度优先搜索（递归）

四、对称二叉树

思路：递归

五、完全二叉树的节点个数

思路：递归

六、平衡二叉树

思路：递归

七、二叉树的所有路径

思路1：深度优先搜索（递归）

思路2：广度优先搜索

八、左叶子之和

思路1：深度优先搜索

思路2：广度优先搜索

九、找树左下角的值

思路1：广度优先搜索

十、路径总和

思路：广度优先搜索

思路：深度优先搜索（回溯）

十一、从中序与后序遍历序列构造二叉树

思路：递归

思路：递归

总结

十二、最大二叉树

思路：递归

十三、合并二叉树

思路：深度优先搜索

十四、二叉树搜索树

思路：递归

思路：中序遍历

思路：递归

思路：中序遍历+递归

十五、二叉树的最近公共祖先

思路：回溯

十六、二叉搜索树中的插入操作

思路

十七、删除二叉搜索树中的节点

思路

十八、修剪二叉搜索树

思路 递归

十九、将有序数组转换为二叉搜索树

思路：递归

二十、把二叉搜索树转换为累加树

思路：反中序遍历

思路递归