每日一题——May

Posted on 2022-05-01 Edited on 2023-02-24 In Java Word count in article: 16k Reading time ≈ 14 mins.

前言

5月份每日一题记录~

1305. 两棵二叉搜索树中的所有元素

给你 root1 和 root2 这两棵二叉搜索树。请你返回一个列表，其中包含 两棵树 中的所有整数并按升序排序。.

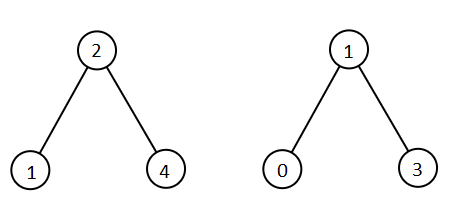
1 2	输入：root1 = [2,1,4], root2 = [1,0,3] 输出：[0,1,1,2,3,4]

思路：中序遍历+归并

回顾二叉搜索树的定义：

当前节点的左子树中的数均小于当前节点的数；
当前节点的右子树中的数均大于当前节点的数；
所有左子树和右子树自身也是二叉搜索树。

根据上述定义，我们可以用中序遍历访问二叉搜索树，即按照访问左子树——根节点——右子树的方式遍历这棵树，而在访问左子树或者右子树的时候也按照同样的方式遍历，直到遍历完整棵树。遍历结束后，就得到了一个有序数组。

由于整个遍历过程天然具有递归的性质，我们可以直接用递归函数来模拟这一过程。具体描述见 94. 二叉树的中序遍历的官方题解。

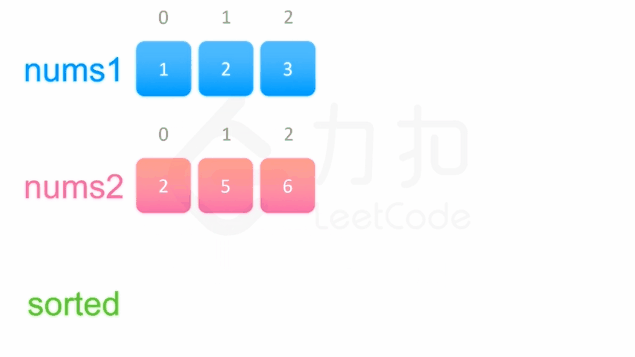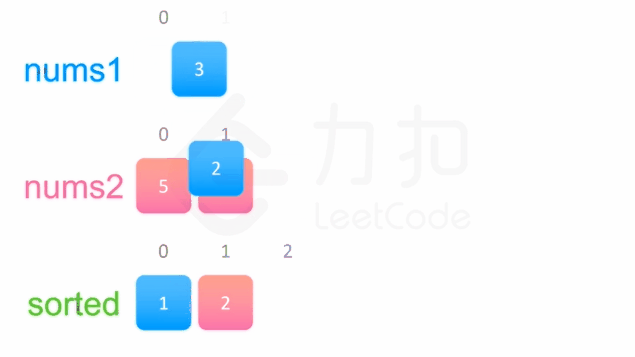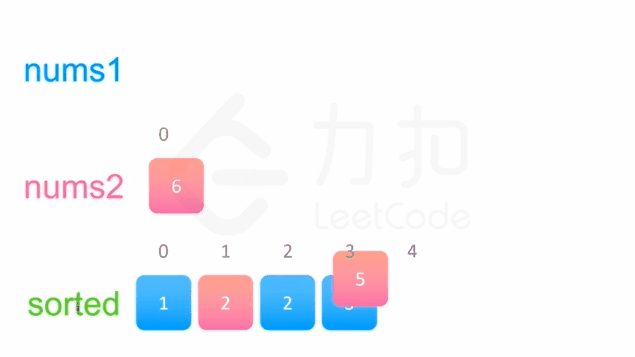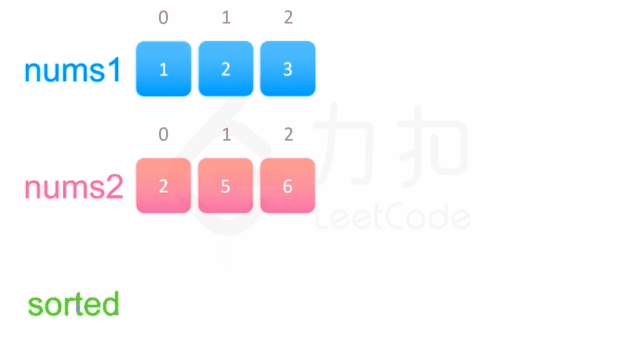
中序遍历这两棵二叉搜索树，可以得到两个有序数组。然后可以使用双指针方法来合并这两个有序数组，这一方法将两个数组看作两个队列，每次从队列头部取出比较小的数字放到结果中（头部相同时可任取一个）。如下面的动画所示：

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public List<Integer> getAllElements(TreeNode root1, TreeNode root2) {
        List<Integer> nums1 = new ArrayList<Integer>();
        List<Integer> nums2 = new ArrayList<Integer>();
        inorder(root1,nums1);
        inorder(root2,nums2);

        List<Integer> ans = new ArrayList<Integer>();
        int p1 = 0 ,p2 = 0;
        while(true){
            if(p1 == nums1.size()){
                ans.addAll(nums2.subList(p2,nums2.size()));
                break;
            }
            if(p2 == nums2.size()){
                ans.addAll(nums1.subList(p1,nums1.size()));
                break;
            }
            if(nums1.get(p1) < nums2.get(p2)){
                ans.add(nums1.get(p1++));
            }else{
                ans.add(nums2.get(p2++));
            }
        }
        return ans;
    }

    public void inorder(TreeNode root , List<Integer> res){
        if(root != null){
            inorder(root.left,res);
            res.add(root.val);
            inorder(root.right,res);
        }
    }
}

执行用时：17 ms, 在所有 Java 提交中击败了65.99%的用户，O（m+n），其中 n 和 m分别为两棵二叉搜索树的节点个数
内存消耗：43.8 MB, 在所有 Java 提交中击败了35.23%的用户，O（m+n）
通过测试用例：48 / 48

937. 重新排列日志文件

给你一个日志数组 logs。每条日志都是以空格分隔的字串，其第一个字为字母与数字混合的标识符。

有两种不同类型的日志：

字母日志：除标识符之外，所有字均由小写字母组成
数字日志：除标识符之外，所有字均由数字组成
请按下述规则将日志重新排序：

所有字母日志都排在数字日志之前。
字母日志在内容不同时，忽略标识符后，按内容字母顺序排序；在内容相同时，按标识符排序。
数字日志应该保留原来的相对顺序。
返回日志的最终顺序。

输入：logs = [“dig1 8 1 5 1”,”let1 art can”,”dig2 3 6”,”let2 own kit dig”,”let3 art zero”]
输出：[“let1 art can”,”let3 art zero”,”let2 own kit dig”,”dig1 8 1 5 1”,”dig2 3 6”]
解释：
字母日志的内容都不同，所以顺序为 “art can”, “art zero”, “own kit dig” 。
数字日志保留原来的相对顺序 “dig1 8 1 5 1”, “dig2 3 6” 。

思路：定义类+排序

这个题是一个直接模拟的题目，但个人觉得困难在于实现，写的时候也是参考了官方解写的。。

根据题意自定义排序的比较方式。比较时，先将数组日志按照第一个空格分成两部分字符串，其中第一部分为标识符。第二部分的首字符可以用来判断该日志的类型。两条日志进行比较时，需要先确定待比较的日志的类型，然后按照以下规则进行比较：

字母日志始终小于数字日志。
数字日志保留原来的相对顺序。当使用稳定的排序算法时，可以认为所有数字日志大小一样。当使用不稳定的排序算法时，可以用日志在原数组中的下标进行比较。
字母日志进行相互比较时，先比较第二部分的大小；如果相等，则比较标识符大小。比较时都使用字符串的比较方式进行比较。

定义比较函数logCompare 时，有两个输入 log 1和 log 2 。当相等时，返回 0；当 log 1大时，返回正数；当 log 2大时，返回负数。

class Solution {
    public String[] reorderLogFiles(String[] logs) {
        int len = logs.length;
        Pair[] arr = new Pair[len];
        for(int i = 0 ; i<len ; i++){
            arr[i] = new Pair(logs[i],i);
        }
        Arrays.sort(arr,(a,b) -> logCompare(a,b));
        String[] ans = new String[len];
        for(int i = 0 ; i<len ; i++){
            ans[i] = arr[i].log;
        }
        return ans;
    }

    public int logCompare(Pair pair1, Pair pair2){
        String log1 = pair1.log , log2 = pair2.log;
        int index1 = pair1.index , index2 = pair2.index;
        //将数组以空格分割为两段，第一段为标识符
        String[] split1 = log1.split(" ",2);
        String[] split2 = log2.split(" ",2);
        //判断第二段是字母日志还是数字日志
        boolean isDigit1 = Character.isDigit(split1[1].charAt(0));
        boolean isDigit2 = Character.isDigit(split2[1].charAt(0));

        if(isDigit1 && isDigit2){
            //如果都为数字日志
            return index1 - index2;
        }
        if(!isDigit1&&!isDigit2){
            //如果都为字母日志
            int sc = split1[1].compareTo(split2[1]);
            if(sc!=0){
                return sc;
            }
            //如果第二段相等，则比较标识符
            return split1[0].compareTo(split2[0]);
        }
        //如果pair1为数字日志，其始终比字母日志大，所以直接返回1
        return isDigit1?1:-1;
    }

    class Pair{
        String log;
        int index;

        public Pair(String log, int index){
            this.log = log;
            this.index = index;
        }
    }
}

执行用时：5 ms, 在所有 Java 提交中击败了82.98%的用户,O*(nlog*n)，其中 n 是 logs 的字符数，是平均情况下内置排序的时间复杂度
内存消耗：41.3 MB, 在所有 Java 提交中击败了92.73%的用户
通过测试用例：65 / 65

1823. 找出游戏的获胜者

共有 n 名小伙伴一起做游戏。小伙伴们围成一圈，按顺时针顺序从 1 到 n 编号。确切地说，从第 i 名小伙伴顺时针移动一位会到达第 (i+1) 名小伙伴的位置，其中 1 <= i < n ，从第 n 名小伙伴顺时针移动一位会回到第 1 名小伙伴的位置。

游戏遵循如下规则：

从第 1 名小伙伴所在位置开始。
沿着顺时针方向数 k 名小伙伴，计数时需要包含起始时的那位小伙伴。逐个绕圈进行计数，一些小伙伴可能会被数过不止一次。
你数到的最后一名小伙伴需要离开圈子，并视作输掉游戏。
如果圈子中仍然有不止一名小伙伴，从刚刚输掉的小伙伴的顺时针下一位小伙伴开始，回到步骤 2 继续执行。
否则，圈子中最后一名小伙伴赢得游戏。
给你参与游戏的小伙伴总数 n ，和一个整数 k ，返回游戏的获胜者。

思路1：队列+模拟

使用队列存储圈子中的小伙伴编号，初始时将 1 到 n 的所有编号依次加入队列，队首元素即为第 1 名小伙伴的编号。

每一轮游戏中，从当前小伙伴开始数 k 名小伙伴，数到的第 k 名小伙伴离开圈子。模拟游戏过程的做法是，将队首元素取出并将该元素在队尾处重新加入队列，重复该操作 k - 1 次，则在 k - 1次操作之后，队首元素即为这一轮中数到的第 k 名小伙伴的编号，将队首元素取出，即为数到的第 k 名小伙伴离开圈子。上述操作之后，新的队首元素即为下一轮游戏的起始小伙伴的编号。

class Solution {
    public int findTheWinner(int n, int k) {
        Queue<Integer> queue = new ArrayDeque<Integer>();
        for(int i = 1 ; i <= n ; i++){
            queue.offer(i);
        }
        while(queue.size() > 1 ){
            for(int i = 1 ; i < k ; i++){
                queue.offer(queue.poll());
            }
            queue.poll();
        }
        return queue.peek();
    }
}

执行用时：24 ms, 在所有 Java 提交中击败了24.43%的用户
内存消耗：38.6 MB, 在所有 Java 提交中击败了33.60%的用户
通过测试用例：95 / 95

713. 乘积小于 K 的子数组

给你一个整数数组 nums 和一个整数 k ，请你返回子数组内所有元素的乘积严格小于 k 的连续子数组的数目。

输入：nums = [10,5,2,6], k = 100
输出：8
解释：8 个乘积小于 100 的子数组分别为：[10]、[5]、[2],、[6]、[10,5]、[5,2]、[2,6]、[5,2,6]。
需要注意的是 [10,5,2] 并不是乘积小于 100 的子数组。

思路：滑动窗口

一个简单的滑动窗口应用题目

class Solution {
    public int numSubarrayProductLessThanK(int[] nums, int k) {
        int len = nums.length , ans = 0;
        if(k <= 1){
            return 0;
        }
        for(int i = 0 ,j = 0 ,cur = 1 ; i < len ; i++){
            cur *= nums[i];
            while(cur >= k){
                cur /= nums[j++];
            }
            ans += i - j + 1;
        }
        return ans;
    }
}

执行用时：4 ms, 在所有 Java 提交中击败了99.95%的用户
内存消耗：48 MB, 在所有 Java 提交中击败了35.07%的用户
通过测试用例：97 / 97

933. 最近的请求次数

写一个 RecentCounter 类来计算特定时间范围内最近的请求。

请你实现 RecentCounter 类：

RecentCounter() 初始化计数器，请求数为 0 。
int ping(int t) 在时间 t 添加一个新请求，其中 t 表示以毫秒为单位的某个时间，并返回过去 3000 毫秒内发生的所有请求数（包括新请求）。确切地说，返回在 [t-3000, t] 内发生的请求数。
保证每次对 ping 的调用都使用比之前更大的 t 值。

输入：
[“RecentCounter”, “ping”, “ping”, “ping”, “ping”]
[[], [1], [100], [3001], [3002]]
输出：
[null, 1, 2, 3, 3]

解释：
RecentCounter recentCounter = new RecentCounter();
recentCounter.ping(1); // requests = [1]，范围是 [-2999,1]，返回 1
recentCounter.ping(100); // requests = [1, 100]，范围是 [-2900,100]，返回 2
recentCounter.ping(3001); // requests = [1, 100, 3001]，范围是 [1,3001]，返回 3
recentCounter.ping(3002); // requests = [1, 100, 3001, 3002]，范围是 [2,3002]，返回 3

思路：队列

我们可以用一个队列维护发生请求的时间，当在时间 tt 收到请求时，将时间 tt 入队。

由于每次收到的请求的时间都比之前的大，因此从队首到队尾的时间值是单调递增的。当在时间 tt 收到请求时，为了求出 [t-3000,t][t−3000,t] 内发生的请求数，我们可以不断从队首弹出早于 t-3000 的时间。循环结束后队列的长度就是 [t-3000,t][t−3000,t] 内发生的请求数。

class RecentCounter {
    Queue<Integer> queue ;

    public RecentCounter() {
        queue = new  ArrayDeque<Integer>();
    }
    
    public int ping(int t) {
        queue.offer(t);
        while(queue.peek() < t-3000){
            queue.poll();
        }
        return queue.size();
    }
}

执行用时：24 ms, 在所有 Java 提交中击败了20.16%的用户
内存消耗：49.1 MB, 在所有 Java 提交中击败了87.08%的用户
通过测试用例：68 / 68

942. 增减字符串匹配

由范围 [0,n] 内所有整数组成的 n + 1 个整数的排列序列可以表示为长度为 n 的字符串 s ，其中:

如果 perm[i] < perm[i + 1] ，那么 s[i] == ‘I’
如果 perm[i] > perm[i + 1] ，那么 s[i] == ‘D’
给定一个字符串 s ，重构排列 perm 并返回它。如果有多个有效排列perm，则返回其中任何一个。

示例 1：

输入：s = “IDID”
输出：[0,4,1,3,2]

思路：贪心+双指针

该做法成立的本质为：始终确保可用数是连续段，每次选择位于边界的数进行构造，可以直接确保当前构造回合的正确性，从而让边界情况的归纳推理可以运用到每个构造回合。

考虑 \textit{perm}[0]perm[0] 的值，根据题意：

如果 s[0]=‘I’，那么令perm[0]=0，则无论 perm[1] 为何值都满足 perm[0]<perm[1]；
如果s[0]=‘D’，那么令 perm[0]=n，则无论perm[1] 为何值都满足 perm[0]>perm[1]；

确定好perm[0] 后，剩余的 n−1 个字符和 n个待确定的数就变成了一个和原问题相同，但规模为 n−1 的问题。因此我们可以继续按照上述方法确定 perm[1]：如果s[1]=‘I’，那么令 perm[1] 为剩余数字中的最小数；如果 s[1]=‘D’，那么令 perm[1] 为剩余数字中的最大数。如此循环直至剩下一个数，填入perm[n] 中。

class Solution {
    public int[] diStringMatch(String s) {
        int len = s.length() , left = 0 , right = len;
        int[] ans = new int[len+1];
        for(int i = 0 ; i<len ; i++){
            ans[i] = s.charAt(i) == 'I'?left++:right--;
        }
        ans[len] = left;
        return ans;
    }
}

执行用时：2 ms, 在所有 Java 提交中击败了87.44%的用户,O(n)
内存消耗：41.9 MB, 在所有 Java 提交中击败了36.45%的用户,O(1)
通过测试用例：95 / 95

944. 删列造序

给你由 n 个小写字母字符串组成的数组 strs，其中每个字符串长度相等。

这些字符串可以每个一行，排成一个网格。例如，strs = [“abc”, “bce”, “cae”] 可以排列为：
1
2
3
abc
bce
cae
你需要找出并删除不是按字典序升序排列的列。在上面的例子（下标从 0 开始）中，列 0（’a’, ‘b’, ‘c’）和列 2（’c’, ‘e’, ‘e’）都是按升序排列的，而列 1（’b’, ‘c’, ‘a’）不是，所以要删除列 1 。

返回你需要删除的列数。
1
2
3
4
5
6
7
8
9
示例 1：

输入：strs = ["cba","daf","ghi"]
输出：1
解释：网格示意如下：
  cba
  daf
  ghi
列 0 和列 2 按升序排列，但列 1 不是，所以只需要删除列 1 。

思路：直接模拟

class Solution {
    public int minDeletionSize(String[] strs) {
        int row = strs.length,col = strs[0].length() ,ans = 0;
        for(int j = 0 ; j < col ; j++){
            for(int i = 1 ; i < row ; i++){
                if(strs[i - 1].charAt(j) > strs[i].charAt(j)){
                    ans++;
                    break;
                }
            }
        }
        return ans;
    }
}

时间复杂度：O（row x col）
空间复杂度：O（1）

面试题 01.05. 一次编辑

字符串有三种编辑操作:插入一个字符、删除一个字符或者替换一个字符。给定两个字符串，编写一个函数判定它们是否只需要一次(或者零次)编辑。
1
2
3
4
5
6
示例 1:

输入: 
first = "pale"
second = "ple"
输出: True

思路：双指针分情况模拟

为了方便，我们令first、 second，两者长度为 n 和 m，并让 first为两种中的长度较短的那个（若 second 较短，则将两者交换）。

接下来是简单的双指针处理（使用 count 记录操作次数）：

我们最多使用不超过一次的操作，因此如果∣n−m∣>1，直接返回 False；
若两者长度差不超过 1，使用 i 和 j分别指向两字符的最左侧进行诸位检查：
- 若 first[i] = second[j]，让 i 和 j 继续后移进行检查；
- 若 first[i] !=second[j]，根据两字符串长度进行分情况讨论：
  - 若 n = m，说明此时只能通过「替换」操作消除不同，分别让 i 和 j 后移，并对 count 进行加一操作；
  - 若 n !=m，由于我们人为确保了 first 更短，即此时是 n < m，此时只能通过对 first 字符串进行「添加」操作来消除不同，此时让 j 后移，i 不动（含义为在 first字符串中的 i 位置增加一个 b[j] 字符），并对 count 进行加一操作。

最终我们根据 count 是否不超过 11 来返回结果。

class Solution {
    public boolean oneEditAway(String first, String second) {
        int n = first.length() , m = second.length();
        if(Math.abs(m - n )> 1) return false;
        if(n > m ) return oneEditAway(second , first);
        int i = 0 , j = 0 , count = 0;
        while(i < n && j < m && count <= 1){
            if(first.charAt(i) == second.charAt(j)){
                i++;
                j++;
            }else{
                if(n == m){
                    i++;
                    j++;
                    count++;
                }else{
                    j++;
                    count++;
                }
            }
        }
        return count <= 1;
    }
}

时间复杂度：令 n和 m 分别为两字符串长度，复杂度为 O*(max(n,m))
空间复杂度：O(1)

面试题 04.06. 后继者

设计一个算法，找出二叉搜索树中指定节点的“下一个”节点（也即中序后继）。

如果指定节点没有对应的“下一个”节点，则返回null。

示例 1:

输入: root = [2,1,3], p = 1

2
/
1 3

输出: 2

思路：二叉搜索树

利用二叉树搜索的性质

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    public TreeNode inorderSuccessor(TreeNode root, TreeNode p) {
        int target = p.val;
        TreeNode cur = root;
        TreeNode ans = null;
        while(cur!=null){
            if(cur.val > target){
                ans = cur;
                cur = cur.left;
            }else{
                cur = cur.right;
            }
        }
        return ans;
    }
}

时间复杂度：O(n)，其中 n 是二叉搜索树的节点数。遍历的节点数不超过二叉搜索树的高度，平均情况是 O(logn)，最坏情况是O(n)。
空间复杂度：O(1)。

462. 最少移动次数使数组元素相等 II

给你一个长度为 n 的整数数组 nums ，返回使所有数组元素相等需要的最少移动数。

在一步操作中，你可以使数组中的一个元素加 1 或者减 1 。

示例 1：

输入：nums = [1,2,3]
输出：2
解释：
只需要两步操作（每步操作指南使一个元素加 1 或减 1）：
[1,2,3] => [2,2,3] => [2,2,2]

思路：排序

从感官上而言，将数组进行排序，位于中间的那个数肯定是离所有数的距离和最小的那个数。

class Solution {
    public int minMoves2(int[] nums) {
        Arrays.sort(nums);
        int len = nums.length , ans = 0 , mid = nums[len/2];
        for(int i = 0 ; i < len ; i++){
            ans += Math.abs(nums[i] - mid);
        }
        return ans;
    }
}

965. 单值二叉树

如果二叉树每个节点都具有相同的值，那么该二叉树就是单值二叉树。

只有给定的树是单值二叉树时，才返回 true；否则返回 false。
1
2
输入：[1,1,1,1,1,null,1]
输出：true

思路：深度优先搜索(递归)

一棵树的所有节点都有相同的值，当且仅当对于树上的每一条边的两个端点，它们都有相同的值（这样根据传递性，所有节点都有相同的值）。

因此，我们可以对树进行一次深度优先搜索。当搜索到节点 x 时，我们检查 x 与 x 的每一个子节点之间的边是否满足要求。例如对于左子节点而言，如果其存在并且值与 x相同，那么我们继续向下搜索该左子节点；如果值与x 不同，那么我们直接返回 \text{False}False。

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public boolean isUnivalTree(TreeNode root) {
        if(root == null) return true;
        if(root.left != null){
            if(root.val != root.left.val || !isUnivalTree(root.left)){
                return false;
            }
        }

        if(root.right != null){
            if(root.val != root.right.val || !isUnivalTree(root.right)){
                return false;
            }
        }
        return true;
    }
}

时间复杂度：O(n)，其中 n 是二叉树的节点个数。我们遍历二叉树的每个节点至多一次。
空间复杂度：O(n)，即为深度优先搜索中需要使用的栈空间。

面试题 17.11. 单词距离

有个内含单词的超大文本文件，给定任意两个不同的单词，找出在这个文件中这两个单词的最短距离(相隔单词数)。如果寻找过程在这个文件中会重复多次，而每次寻找的单词不同，你能对此优化吗?

示例：

输入：words = [“I”,”am”,”a”,”student”,”from”,”a”,”university”,”in”,”a”,”city”], word1 = “a”, word2 = “student”
输出：1

思路：一次遍历+双指针

用 index 1和index 2分别表示数组 words 已经遍历的单词中的最后一个word 1的下标和最后一个 word2的下标，初始时 index1 = index2 = -1。遍历数组 words，当遇到 word1或 word 2时，执行如下操作

如果遇到word1，则将index1更新为当前下标；如果遇到word2，则将index2更新为当前下标。
如果index1和index2都为非负，则计算两个下标的距离，并用该距离更新最短距离

遍历结束后即可得到word1和word2的最短距离

class Solution {
    public int findClosest(String[] words, String word1, String word2) {
        int len = words.length;
        int ans = len;
        int index1 = -1 , index2 = -1;
        for(int i = 0 ; i <len-1 ; i++){
            String word = words[i];
            if(word.equals(word1)){
                index1 = i;
            }else if(word.equals(word2)){
                index2 = i;
            }
            if(index1 >= 0 && index2 >= 0){
                ans = Math.min(ans,Math.abs(index1 - index2));
            }
        }
        return ans;
    }
}